A colleague in food science recently sent me a narrative review outlining some of the challenges in their field (Cassidy and Minihane, 2017, Am J Clin Nutr). One of these was “extensive heterogeneity in the response to increased intake [of flavonoids]”.
Response heterogeneity is often highlighted to justify the need for precision medicine. The argument is that we need precision medicine to identify and treat the people that we know will respond well to a particular treatment, and not bother treating those who won’t respond. Sounds smart. The problem however is that the studies used to demonstrate response heterogeneity simply don’t, and doing it the right way is much more challenging than people seem to understand.
Have a look at the figure below. The data are from a randomized controlled trial of a 1-year flavonoid intervention. More specifically, each data-point in the plot is one of the participants that was randomized to the intervention arm of the trial. You can see that the mean 12-month change in fasting insulin was -0.72 mU/L in those participants (the dash-dot horizontal line). You will also notice how variable those changes are: they range from -8 to +6 mU/L, and almost half of participants actually experienced an increase in fasting insulin over the course of the study.
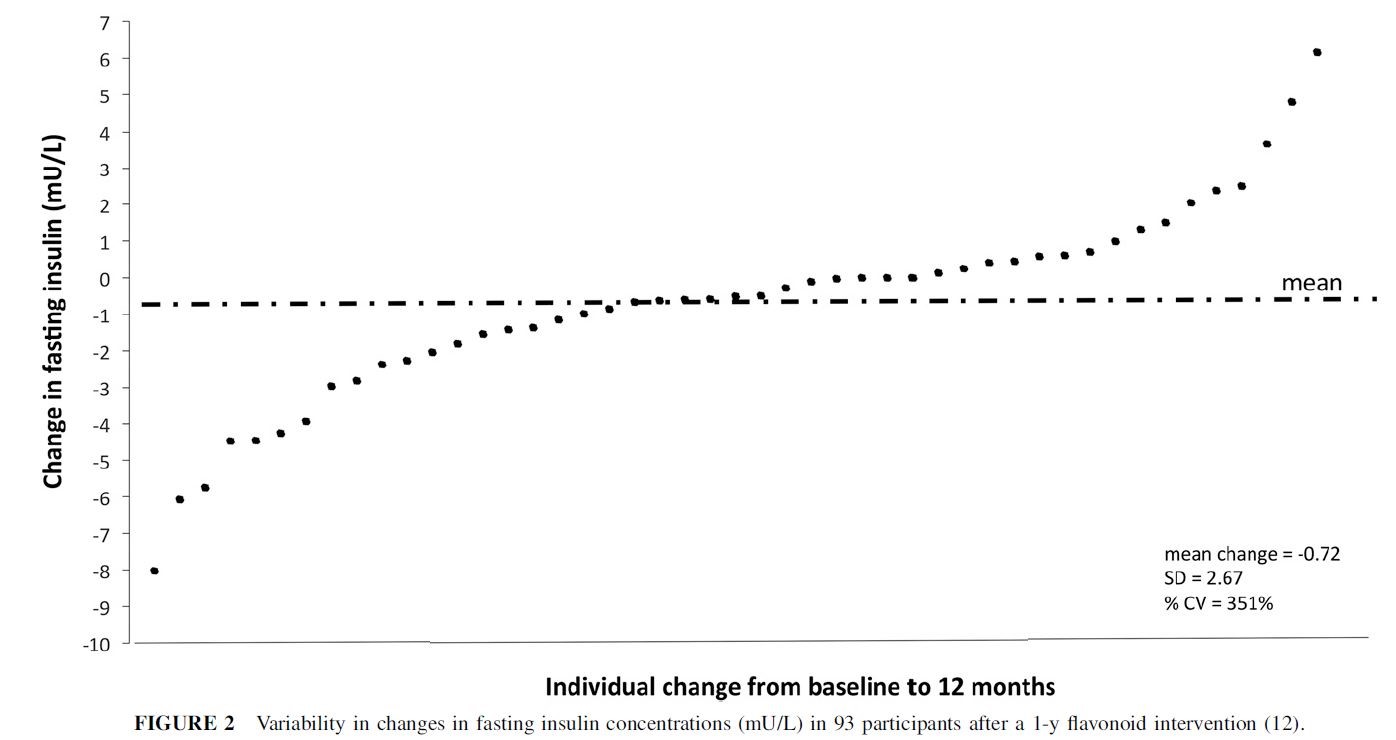
Can we learn anything else from this plot? Not really, as I’ll explain below. However, some people look at it and want to ascribe all of that variability in fasting insulin to differences in how participants responded to the treatment. For example, Cassidy and Minihane interpret it as demonstrating “a large variability in the physiologic response to flavonoid intake” and that the figure above “shows the insulin response to the previously mentioned 1-y intervention” [emphasis mine]. In other words, they think that the drug caused some people to experience an increase in fasting insulin, while in others it caused a decrease. Unfortunately, at least for proponents of personalized medicine, it does no such thing, which I will now try to explain.
To further interpret the plot above, we need one more critical piece of information - the outcomes of the control group. Without that information, you might be tempted to conclude that the treatment had the effect of lowering fasting insulin by 0.72 mU/L, on average. But what if we saw the exact same thing in the control group? What would you conclude then? This is the fundamental point of an RCT – our inferences about treatment effects are based on treatment comparisons, so we can’t say anything about the effect of the treatment without reference to what happened in the control group.
This is just as true if we want to say something about the response of a particular patient. Unfortunately, there is no way to obtain such a control observation. I would need to need to give a person the treatment, observe the outcome, reset the entire universe to the exact condition it was in when I gave them the treatment, and then withhold the treatment and see what happens. The effect of the treatment for that patient would then be apparent in the difference in the outcomes measured under the two conditions.
This kind of mental experiment reflects the counterfactual interpretation of causality. It “works” because if we see a difference in outcomes, it could only be explained the difference in treatment conditions, since everything else is exactly the same (1).
Moving back into reality, we could take two people, give the treatment to one but not the other, and then compare their outcomes. Would you believe that the difference in their outcomes was a measurement of the treatment effect? Of course not, because it’s a near certainty that the two people will differ in important ways that influence the outcome, irrespective of their treatment condition.
Since this can’t work with just two people, let’s give the different treatments to different groups of people. If I then then compared the average outcome in each group, should you then accept that it’s a good estimate of the treatment effect?
The answer depends on your opinion about the exchangeability of the two groups. By exchangeability, I mean that the distribution of future outcomes under the control condition is the same in both groups. Importantly, I don’t need everything about the two groups to be identical - just the distribution of future outcomes.
Since we can’t know the future outcome for each person, we can’t directly create exchangeable groups. However, through clever study design we can often create groups that we are happy to assume are exchangeable by controlling for the factors we expect to affect the outcome. For example, in study of mice we might use genetically identical animals, keep them in the exact same environment, feed them the exact same food, etc.
It’s clearly trickier in humans. Thankfully we have a good way to create exchangeable groups of humans – randomization. As people enter the trial, we randomly allocate them to treatment arms, with no consideration of patient/clinician/clinic or other characteristics. If we have a good idea of how the eventual outcomes might be distributed under the different conditions (e.g. what is the distribution of fasting glucose in the types of patients being recruited into the trial?), we can randomize enough people to feel confident that the groups will indeed be exchangeable.
So where does this leave us with trying to demonstrate response heterogeneity? For the vast majority of study designs, including the parallel arm trial described above, you can’t. The RCT result is inherently limited. It gives us our best guess at what the average treatment effect is, and we are forced to act as if all patients will similarly experience that effect, even though we know they won’t.
Proponents of personalized medicine would like to find a way to move beyond this dissatisfying situation. Unfortunately, they will need to face some hard truths. As far as I can see, there are only two ways to scientifically demonstrate something close to response heterogeneity.
The first will hinge on our ability to identify and recruit large enough groups of patients that share the characteristics we suspect are driving response heterogeneity (i.e. gene X). The challenge however is getting enough people who meet the necessary conditions, when they are going to be quite rare by definition. To put this challenge in context, trials are often criticized for not being large enough to estimate subgroup specific effects. Well, if we can’t often run studies that let us estimate the effect of a treatment in a subgroup that makes up 30% of possible patients, for example, how are we going to run studies in subgroups that make up fewer than 0.01% of those patients?
The other option is to run repeated-crossover and N-of-1 trials where individuals are repeatedly exposed to the different treatments. However, that’s only possible for particular combinations of interventions and outcomes.
NOTES
I was introduced to this problem though the work of Professor Stephen Senn. To learn more, see this video, and this excellent paper in Statistics in Medicine, Mastering variation: variance components and personalised medicine.
(1) - Thankfully we can relax this scenario a bit - we don’t actually need both universes to be exactly the same in every way, since there will be lots of things that don’t have any influence on the outcome. For example, the position of Jupiter could vary between the two universes and we would still get the same difference in outcomes. While this updated scenario would mean less work for an all-powerful deity capable of doing all of this, it remains well out of our reach.
